拉格朗日对偶问题

参考资料：拉格朗日对偶

拉格朗日函数的定义：

拉格朗日对偶的定义：

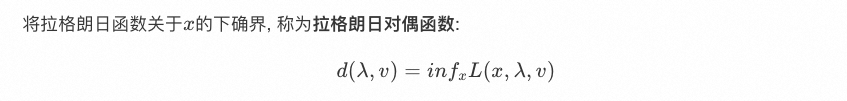
拉格朗日对偶函数一定是一个凹函数，因为仿射函数的下界一定是凹的。

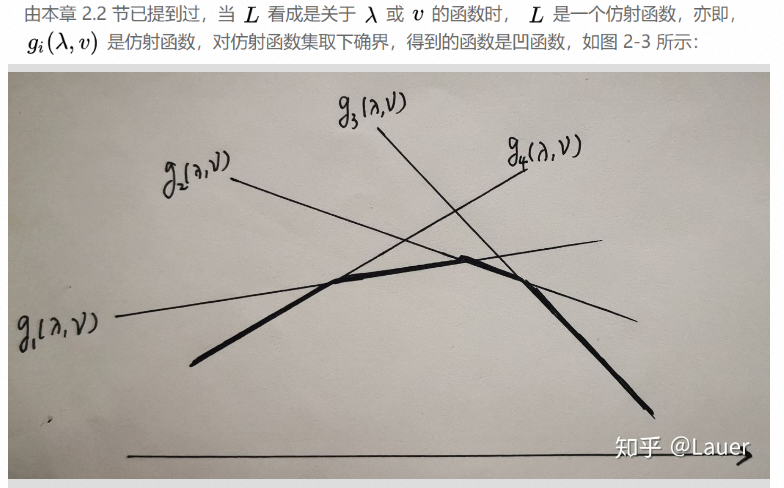
明确拉格朗日对偶的作用：

• 原优化问题比较难求解的情况下(存在约束)，就可以将其转化为拉格朗日对偶问题，对偶问题一定是一个凸问题。但值得注意的是，对偶问题得到的求解是原问题的下界(弱对偶)。

  

那什么情况下是强对偶，也就是对偶问题的最优解即为原问题的最优解？很遗憾, 没有通用的判断条件判断一个问题是否具有强对偶性, 但是很多成果给出了除凸性条件之外的强对偶性成立的条件.

一个比较典型的强对偶的充分条件就是：

• 原问题为凸问题，并且满足slater条件，那么就强对偶就成立。事实上，大部分情况都满足这个条件。

  

KKT则是强对偶的必要条件，也就是满足了强对偶，就一定满足KKT条件，我们就可以以此来求解原问题的最优解。KKT条件如下：

有了KKT条件后，我们一般的求解流程就是：