强化学习基本知识点整理
最近研究黑盒优化问题的时候,发现有方法就是借鉴强化学习的思路: 通过reward的反馈,来优化一个不相干的网络(参数与目标无法直接梯度求导),这个思路在很多地方被反复用到,就像梯度下降一样是个比较经典的想法。因此重新看了一遍强化学习的知识,这一遍看完终于基本梳理清楚了其中的公式推导原理及流程,特此记录。
参考资料: 动手学习强化学习
基本概念
强化学习在本质上是一个马尔科夫决策过程(MDP),由元组

值得注意的是:
- 马尔科夫奖励过程(MRP)就是没有动作MDP
- 多臂老虎机也是个特殊的MDP,相当于没有状态,没有状态转移概率。
在整个MDP过程中,我们最终关注的价值函数有两个:
- 状态价值函数V(s): 从状态s出发到未来为止,能得到的所有reward。
- 动作状态价值函数Q(s, a): 在状态s下执行动作a,到未来为止,能得到的所有reward。

强化学习的目标通常是找到一个策略,使得智能体从初始状态出发能获得最多的期望回报。

求解方法
model-based
所谓的model-based方法,就是指MDP的状态转移函数已知。
在这个情况下,求解状态价值V(s)和动作状态价值Q(s,a)的方法有:
解析解:直接可以通过贝尔曼方程得到解析解,只不过在状态空间大的情况下,求解会比较复杂
蒙特卡洛方法:说到底就是基于概率做采样,通过采样的样本做增量更新:

但是随着策略的不同,V和Q也会不一样,如何求解最优策略呢?这里就可以用到动态规划方法,其方法本质就是将问题拆分成子问题,利用贝尔曼方程做递推公式来更新,具体方法也分为两种:
- 策略迭代:先通过策略评估更新V(s),然后通过策略迭代选取V下最优的策略
- 价值迭代:直接一步到位,每一步都通贝尔曼最优方程来递推更新最优的V
model-free
在真实环境中,状态转移概率往往是未知的,在这种情况下,智能体只能和环境进行交互,通过采样到的数据来学习,这类学习方法统称为无模型的强化学习(model-free reinforcement learning)。
在这种情况下,存在两种比较经典的算法,Sarsa和Q-learning。这两种算法的本质就是通过时序差分的方式去更新Q函数,获取Q函数后即可获取最优策略。
Sarsa:

Q-learning

两者算法的核心区别就在于:在计算下一个动作的Q值时,sarsa还是用相同greedy策略来获取动作,它需要获取(s(t), a(t), r(t), s(t+1), a(t+1))的采样元组,并且在此基础上不断延续上一个r和a持续更新;而Q-learning用的是不同的策略(取max的动作),它只需要获取(s(t), a(t), r(t), s_(t+1))即可,也不需要延续上一个r和a持续更新,他可以将采样得到的这些元组重复利用,重复去更新Q。
因此我们将类似sarsa的这种称为on-policy(在线策略),而Q-learning为off-policy(离线策略),离线策略算法能够重复使用过往训练样本,往往具有更小的样本复杂度,也因此更受欢迎。
Dyna-Q就是在Q-learning上的改进,每次随机选择历史存的样本进行更新:

DQN
传统的Q-learning下,如果状态空间特别大或者状态为连续值,那么需要存储的Q table将会很爆炸,因此之后人们采用了深度神经网络的形式来存储Q table。
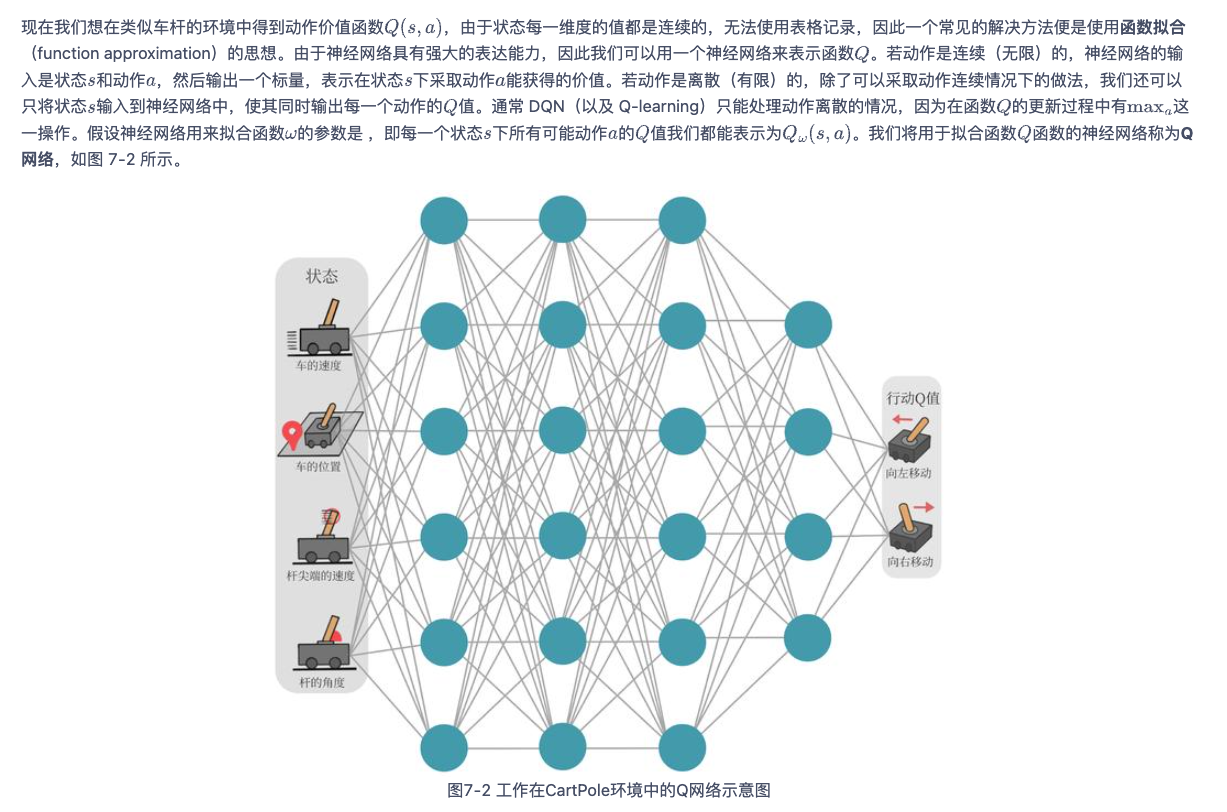
而DQN的损失函数也可以通过Q-learning的更新公式推出:

为了保证训练的稳定性和高效性,DQN 算法引入了经验回放和目标网络两大模块:
- 经验回放:具体做法为维护一个回放缓冲区,将每次从环境中采样得到的四元组数据(状态、动作、奖励、下一状态)存储到回放缓冲区中,训练 Q 网络的时候再从回放缓冲区中随机采样若干数据来进行训练。
- 目标网络: 训练过程中Q网络的不断更新会导致目标不断发生改变,不如暂时先将 TD 目标中的 Q 网络固定住。为了实现这一思想,我们需要利用两套 Q 网络,其中目标网络使用训练网络的一套较旧的参数,训练网络在训练中的每一步都会更新,而目标网络的参数每隔C步才会与训练网络同步一次。
由于DQN的训练比较不稳定,在DQN的基础上还有一些演进:
- Double DQN:思想是为了解决DQN的过高估计

- Dueling DQN:核心是让Q网络多学一个对状态函数的估计,每一次更新时,状态函数都会被更新,这也会影响到其他动作的值。
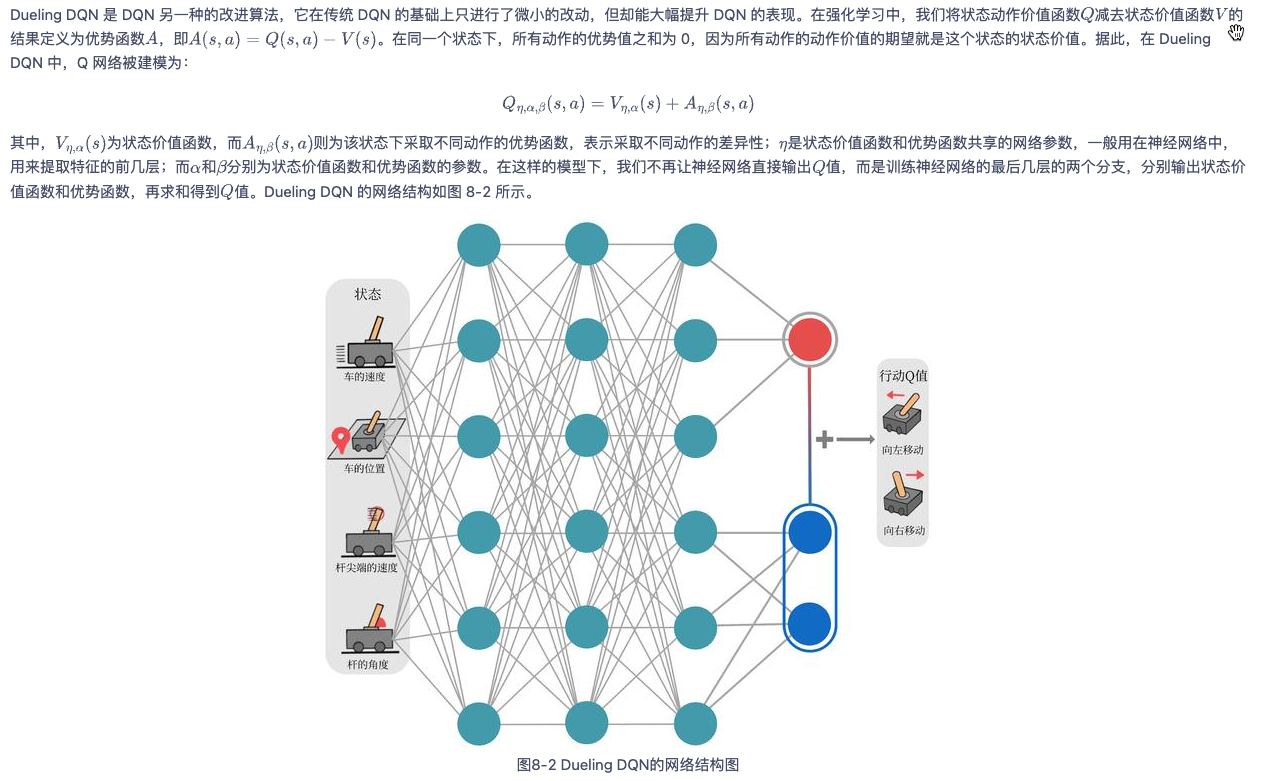
策略梯度
策略梯度算法事实上也是model-free的方法,不过他是一种policy-based的算法,之前所提的sarsa和Q-learning是value-based,并且这个算法的思想就是我在本文开头中提到的黑盒优化思想,所以单独起一章。
- value-based: 主要是学习值函数,然后根据值函数导出一个策略,学习过程中并不存在一个显式的策略
- policy-based: 直接显式地学习一个目标策略
具体而言,策略梯度算法就是直接建模一个神经网络,输入为状态,输出是动作的概率(有点像DQN,但是DQN输出Q值,而这里输出的是概率),最终优化目标直接就是最大化状态函数V值。

这里对目标函数的求导就不贴了,可以在参考资料中找到证明过程。再看下实际如何使用策略梯度算法:

可以看到,最终的这个算法流程就是一个典型的黑盒优化: 策略网络输出一个概率和最终的reward没有直接联系,无法梯度求导,而强化学习就在这个情况下,将目标函数为r * log(p),r为样本获取到的常量,通过最大化该目标函数来对p的网络进行参数更新。这个思想在很多其他算法中都有用到。
Actor-Critic算法
在策略梯度算法的基础上,再结合对状态价值函数的估计,就衍生出了actor-critic算法。

本质上讲,在策略梯度算法中,我们需要对Q(s,a)做估计,虽然是无偏的,但是方差会很大,因此我们可以采用一些其他的值来代替Q,因为对整个算法而言,我们只需要捕捉到reward的相对序,而不用关心起绝对值。actor-critic就提出了很多其他的公式来代替Q(s, a)。这样的话,我们可以引入另一个状态网络像Q-learning一样来估计这个网络。

actor就是产生策略的网络,而critic则是产生reward的网络。
除此之外,后续还有很多流行的强化学习算法例如TRPO, PPO, SAC等,本质上也是在这些算法上的演化,详细可看资料。
TRPO算法
神经网络最常遇见的问题就是训练不稳定,actor-critic这些算法也会有这种问题,因为它没有对梯度的学习率做约束,TRPO最大的改进本质上就是对梯度更新值做了约束,让前后两次策略更新的变化在一定约束内,全名就是信任区域策略优化(trust region policy optimization,TRPO)。
区别于传统策略梯度算法的优化目标J(theta),TRPO的优化目标是前后两次J(theta)的差值,最后可以表示为

最优化目标就变为:

该优化公式直观理解其实也很简单:
- 当老策略下A(s,a) > 0 (总和为0)时,新策略应该要让该状态动作概率增加,反之亦然
- 加了约束条件,让新老策略的变化在一定值域内,这样就保证了梯度更新比较稳定
最终TRPO的具体求解还是比较复杂的,涉及到泰勒一阶和二阶近似,以及黑塞矩阵等,就不详细写了,可以看后面演进的PPO求解。
PPO算法
PPO 基于 TRPO 的思想,但是其算法实现更加简单。并且大量的实验结果表明,与 TRPO 相比,PPO 能学习得一样好(甚至更快),这使得 PPO 成为非常流行的强化学习算法。
PPO的优化目标依然不变,只是在约束这块做了简化。主要分为两种方式。
PPO-惩罚

PPO-截断
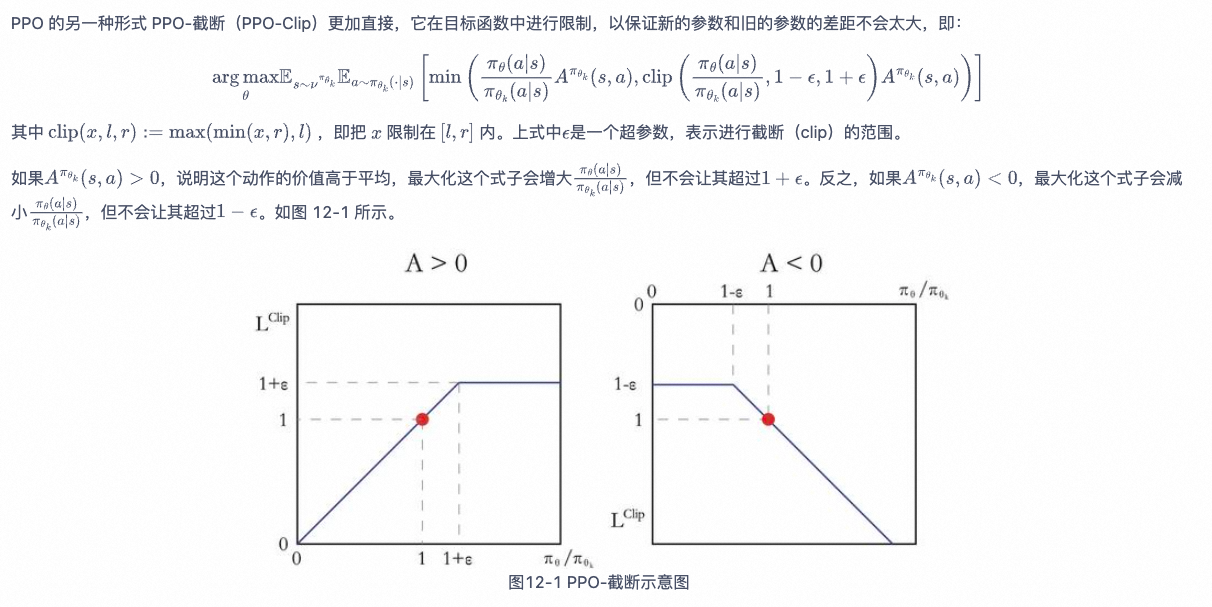
如果我们想要尝试在一个新的环境中使用强化学习算法,那么 PPO 就属于可以首先尝试的算法。