Levy's Blog

优化问题本质上分为凸和非凸两大类。

凸问题有着巨大的优势：

• 成熟有效的求解算法求得全局最优解。(内点法、椭圆法、梯度下降法等)

• 计算复杂度基本上是多项式的，基本是P的。

非凸问题则求解比较困难，实际上大部分的解法都是将非凸问题转化为凸问题。

P，NP，NP-hard， NPC则是计算复杂度的表示。

• P代表多项式内可求解的问题
• NP代表多项式内可验证的问题
• NP-hard表示所有NP问题都可以归约到该问题的问题
• NPC表示即是NP-hard，本身又是NP问题的问题

如果证明P=NP，其实意味着世界上所有的密码系统都被破解了。

因为加密是P的，解密验证是NP的，如果P=NP，说明解密也可以是P的，也就是任何解密算法都可以是多项式内求解的，那么解密就没有时间成本了，随意破解了。

组合优化、混合整数规划等问题一般都是NP-hard问题，例如TSP，背包问题、汉密尔顿回路问题等等。

因为P应该不等NP，这种问题也就是说很难找到多项式时间内的求解算法得到最优解。现在对这些算法的最优求解一般都是指数或者阶乘复杂度的，可参考acm题，算法的话有分支定界之类的。

但如果想要求解近似解，就可以是多项式时间的算法，例如先松弛成凸问题啊之类的。

以前一直以为非凸问题就是没有多项式时间的算法求最优解，其实我理解错了，非凸问题很多都是可以转成凸问题的，例如log-log convex等问题。

典型的一些凸函数：

• 仿射函数
• 绝对值
• 最大值
• p！= 0的所有范数
• 指数函数
• a> 1或者 <0的幂函数
• xlogx
• 以及一系列的保凸运算。。

典型的凸问题(等式约束一定要是仿射的！)：

• 线性规划 （LP）
• 二次规划 (QP)
• 半正定规划(不等式约束为LMI，线性矩阵不等式)(SDP)
• 锥规划(CP)

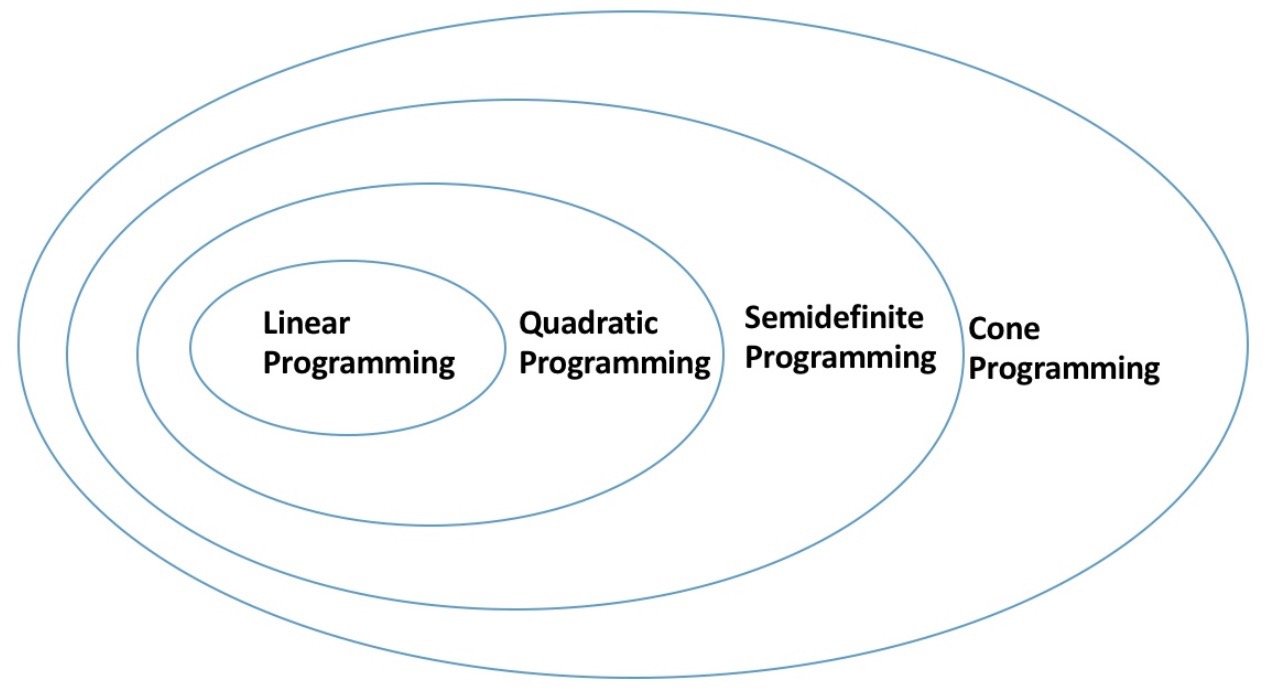
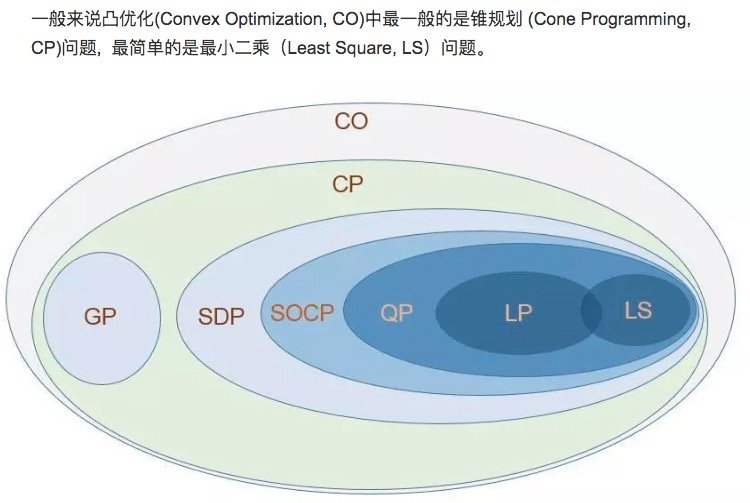
对称的正定矩阵一定代表了是个凸锥。